Сферические функции

Сферические функции представляют собой угловую часть семейства ортогональных решений уравнения Лапласа, записанную в сферических координатах. Они широко используются для изучения физических явлений в пространственных областях, ограниченных сферическими поверхностями и при решении физических задач, обладающих сферической симметрией. Сферические функции имеют большое значение в теории дифференциальных уравнений в частных производных и теоретической физике, в частности в задачах расчёта электронных орбиталей в атоме, гравитационного поля геоида, магнитного поля планет и интенсивности реликтового излучения.

Определение

Вещественные сферические функции Y_lm, l=0…4 (сверху вниз), m=0…4 (слева направо). Функции отрицательного порядка Y_l-m повёрнуты вокруг оси Z на 90/m градусов относительно функций положительного порядка.

Сферические функции являются собственными функциями оператора Лапласа в сферической системе координат (обозначение [math]\displaystyle{ Y_{l}^m(\theta, \varphi) }[/math]). Они образуют ортонормированную систему в пространстве функций на сфере [math]\displaystyle{ \mathbb{S}^2 }[/math] в трёхмерном пространстве:

[math]\displaystyle{ \langle Y_{l}^m; Y_{l}^m \rangle = \iint |Y_{l}^m|^2 \sin{\theta}\,d\theta\,d\varphi = 1 }[/math]

[math]\displaystyle{ \langle Y_{l}^m; Y_{l'}^{m'} \rangle = \int\limits_0^{2 \pi} \int\limits_0^{\pi} Y_{l'}^{m'*} Y_{l}^{m} \sin{\theta}\,d\theta \,d\varphi = \delta_{l l'} \delta_{m m'} }[/math],

где ^* обозначает комплексное сопряжение, [math]\displaystyle{ \delta_{l l'} }[/math] — символ Кронекера.

Сферические функции имеют вид

[math]\displaystyle{ Y_{l}^m= \frac{1}{\sqrt{2 \pi}} e^{i m \varphi} \Theta_{l m}(\theta) }[/math],

где функции [math]\displaystyle{ \Theta_{l m}(\theta) }[/math] являются решениями уравнения

[math]\displaystyle{ \frac{1}{\sin{\theta}} \frac{d}{d\theta}\left(\sin{\theta} \frac{d \Theta_{l m}}{d\theta}\right) - \frac{m^2}{\sin^2{\theta}} \Theta_{l m} + l(l+1) \Theta_{l}^m = 0 }[/math]

и имеют вид

[math]\displaystyle{ \Theta_{l}^m = \sqrt{\frac{2l+1}{2} \frac{(l-m)!}{(l+m)!}} P^m_l (\cos\theta) }[/math]

Здесь [math]\displaystyle{ P^m_l (\cos\theta) }[/math] — присоединённые многочлены Лежандра, а [math]\displaystyle{ m! }[/math] — факториал.

Присоединенные многочлены Лежандра с отрицательным [math]\displaystyle{ m }[/math] здесь вводятся как

[math]\displaystyle{ P_{\ell}^{-m}(x)=(-1)^{m} \frac{(\ell-m) !}{(\ell+m) !} P_{\ell}^{m}(x) }[/math]

Решение уравнения Лапласа в сферических координатах есть так называемая шаровая функция, получаемая умножением сферической функции на решение радиального уравнения.

Вещественная форма

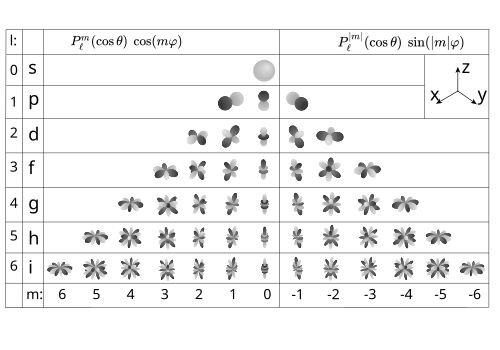
Вещественные сферические функции до шестого порядка

Для сферических функций форма зависимости от угла [math]\displaystyle{ \varphi }[/math] — комплексная экспонента. Используя Формулу Эйлера, можно ввести вещественные сферические функции. Иногда их удобнее использовать в связи с тем, что вещественные функции могут быть наглядно показаны на иллюстрациях, в отличие от комплексных.

[math]\displaystyle{ \begin{align} Y_{\ell m} &= \begin{cases} \displaystyle {i \over \sqrt{2}} \left(Y_\ell^{m} - (-1)^m\, Y_\ell^{-m}\right) & \text{ }\ m\lt 0\\ \displaystyle Y_\ell^0 & \text{ }\ m=0\\ \displaystyle {1 \over \sqrt{2}} \left(Y_\ell^{-m} + (-1)^m\, Y_\ell^{m}\right) & \text{ }\ m\gt 0. \end{cases}\\ &= \begin{cases} \displaystyle \sqrt{2} \, (-1)^m \, \operatorname{Im}[{Y_\ell^{|m|}}] & \text{ }\ m\lt 0\\ \displaystyle Y_\ell^0 & \text{ }\ m=0\\ \displaystyle \sqrt{2} \, (-1)^m \, \operatorname{Re}[{Y_\ell^m}] & \text{ }\ m\gt 0. \end{cases} \end{align} }[/math]

Обратное преобразование:

[math]\displaystyle{ Y_{\ell}^{m} = \begin{cases} \displaystyle {1 \over \sqrt{2}} \left(Y_{\ell |m|} - i Y_{\ell,-|m|}\right) & \text{ }\ m\lt 0 \\ \displaystyle Y_{\ell 0} &\text{ }\ m=0\\ \displaystyle {(-1)^m \over \sqrt{2}} \left(Y_{\ell |m|} + i Y_{\ell,-|m|}\right) & \text{ }\ m\gt 0. \end{cases} }[/math]

Иногда вещественные сферические функции называют зональными, тессеральными и секториальными.^[1]. Функции с m > 0 зависят от угла как косинус, а с m < 0 — как синус.

[math]\displaystyle{ Y_{\ell m} = \begin{cases} \displaystyle (-1)^m\sqrt{2} \sqrt{{2\ell+1 \over 4\pi}{(\ell-|m|)!\over (\ell+|m|)!}} \ P_\ell^{|m|}(\cos \theta) \ \sin( |m|\varphi ) &\mbox{ } m\lt 0 \\ \displaystyle \sqrt{{ 2\ell+1 \over 4\pi}} \ P_\ell^m(\cos \theta) & \mbox{ } m=0 \\ \displaystyle (-1)^m\sqrt{2} \sqrt{{2\ell+1 \over 4\pi}{(\ell-m)!\over (\ell+m)!}} \ P_\ell^m(\cos \theta) \ \cos( m\varphi ) & \mbox{ } m\gt 0 \,. \end{cases} }[/math]

Повороты

Рассмотрим поворот системы координат [math]\displaystyle{ \mathcal R }[/math], на Углы Эйлера [math]\displaystyle{ \alpha, \beta, \gamma, }[/math] который преобрaзует единичный вектор [math]\displaystyle{ \mathbf r }[/math] в вектор [math]\displaystyle{ {\mathbf r}' }[/math]. При этом углы [math]\displaystyle{ \theta', \varphi' }[/math] вектора [math]\displaystyle{ {\mathbf r}' }[/math] в новой системе координат выражаются через углы в старой системе координат следующим образом

[math]\displaystyle{ \cos \theta^{\prime}=\cos \theta \cos \beta+\sin \theta \sin \beta \cos (\varphi-\alpha) }[/math]

[math]\displaystyle{ \operatorname{ctg}\left(\varphi^{\prime}+\gamma\right)=\operatorname{ctg}(\varphi-\alpha) \cos \beta-\frac{\operatorname{ctg} \theta \sin \beta}{\sin (\varphi-\alpha)} }[/math]

В новой системе координат сферическая функция с индексами [math]\displaystyle{ \ell }[/math] и [math]\displaystyle{ m }[/math] будет представима в виде линейной комбинации всех функций с тем же номером [math]\displaystyle{ \ell }[/math] и различными [math]\displaystyle{ m }[/math]. Коэффициентами в линейной комбинации являются комплексно- сопряженные D-матрицы Вигнера^[2]

[math]\displaystyle{ \hat{D}(\alpha, \beta, \gamma) Y_{l}^m(\theta, \varphi)=Y_\ell^m(\theta', \varphi') = \sum_{m' = -\ell}^\ell [D^{(\ell)}_{mm'}(\alpha, \beta, \gamma)]^* Y_\ell^{m'}(\theta, \varphi), }[/math]

Сферические функции с номером [math]\displaystyle{ \ell }[/math] образуют базис неприводимого представления размерности [math]\displaystyle{ (2\ell + 1) }[/math] группы вращений SO(3).

Разложение плоской волны по сферическим функциям

Комплексная экспонента может быть представлена в виде разложения по сферическим функциям

[math]\displaystyle{ e^{i \mathbf{k} \cdot \mathbf{r}}=4 \pi \sum_{l=0}^{\infty} i^{l} j_{l}(k r) \sum_{m=-l}^{l} Y_{l }^{m*}\left(\frac{\mathbf{r}}{|r|}\right) Y_{l}^m\left(\frac{\mathbf{k}}{|k|}\right) }[/math]

Здесь [math]\displaystyle{ j_{n}(x)=\sqrt{\frac{\pi}{2 x}} J_{n+\frac{1}{2}}(x) }[/math] — сферическая функция Бесселя

Разложение произведений сферических функций

Разложения Клебша-Гордана для произведений двух сферических функций выглядят следующим образом ^[3]:

[math]\displaystyle{ Y_{\ell_1}^{m_1}(\Omega) Y_{\ell_2}^{m_2}(\Omega) = \sum_{L, M} \sqrt{\frac{(2 \ell_1 + 1) (2 \ell_2 + 1)}{4 \pi (2 L + 1)}} \langle \ell_1 \, 0 \, \ell_2 \, 0 | L \, 0 \rangle \langle \ell_1 \, m_1 \, \ell_2 \, m_2 | L \, M \rangle Y_L^M (\Omega) }[/math]

См. также

Список сферических функций

Примечания

↑ Тихонов А. Н., Самарский А. А. Уравнения математической физики Архивная копия от 27 декабря 2019 на Wayback Machine
↑ M. A. Morrison, G. A. Parker. A guide to rotations in quantum mechanics Архивная копия от 1 октября 2019 на Wayback Machine. — Australian Journal of Physics, Vol. 40, pp. 465, 1987
↑ Варшалович Д. А., Москалёв А. Н., Херсонский В. К. Квантовая теория углового момента. Архивная копия от 11 ноября 2007 на Wayback Machine — Л.: Наука, 1975.

Литература

Ландау Л. Д., Лифшиц Е. М. Квантовая механика (нерелятивистская теория). — Издание 4-е. — М.: Наука, 1989. — 768 с. — («Теоретическая физика», том III). — ISBN 5-02-014421-5. — математические дополнения

Приложения

Ссылки

Spherical harmonics applied to Acoustic Field analysis on Trinnov Audio’s research page
Spherical Harmonics by Stephen Wolfram and Nodal Domains of Spherical Harmonics by Michael Trott, The Wolfram Demonstrations Project
An accessible introduction to spherical harmonics (by J. B. Calvert)
Spherical harmonics entry at Citizendium

[1] Тихонов А. Н., Самарский А. А. Уравнения математической физики Архивная копия от 27 декабря 2019 на Wayback Machine

[2] M. A. Morrison, G. A. Parker. A guide to rotations in quantum mechanics Архивная копия от 1 октября 2019 на Wayback Machine. — Australian Journal of Physics, Vol. 40, pp. 465, 1987

[varsh-3] Варшалович Д. А., Москалёв А. Н., Херсонский В. К. Квантовая теория углового момента. Архивная копия от 11 ноября 2007 на Wayback Machine — Л.: Наука, 1975.

[1]

[2]

[3]